度数分布表とヒストグラムはある集団のデータ(観測値)の特徴をひと目で理解するために作ります。
生のデータは数値の羅列になっていて、ぱっと見ただけでは特徴をつかむことは難しいです。
度数分布表とヒストグラムを作ると、
- どんなデータ(観測値)が多いのか?
- 正規分布を前提にデータを扱えるか?
- 平均値がいいのか?最頻値がいいのか?
などの基本的なことを把握することができます。
つまり、生データを眺めるだけではわからなかったデータの特徴をサクッと知ることができます。
この記事で学べること
今回は生データから、Rを使って度数分布表とヒストグラムを実際に作ってみます。
生データはRのデータセットから引用させていただきますので、その辺りの操作も少し触れます。
最後に、度数分布表とヒストグラムからどのくらいの情報が読み取れるか?を検証してみます。
では、順に進めていきます。
生データをどこから持ってくる?
生データが無いとどうにもならないので、まずはデータを取り込みます。
Rにはデータセットという、無償提供の観測データが収録されています。
この観測データの中から有名な「iris」というあやめの種類と大きさに関するデータを利用します。
利用するにはRのコンソールで次のように入力します。
library(datasets)
これだけでデータを利用する準備が整います。
この状態で次のようにすると、「iris」のすべてのデータを見ることができます。
iris
このデータはあやめのがく片(sepal)と花びら(petal)の長さ(length)と幅(width)を、あやめの種類ごとに調査したデータです。
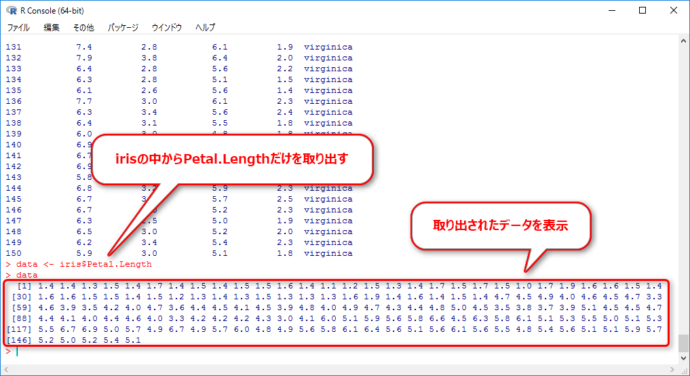
ここでは、どんなデータか?ということはあまり考えずに、このデータの中から花びらの長さ(Petal.Length)だけを取り出します。
data <- iris$Petal.Length data
表示されるのは生データの数字の羅列です。
この情報だけでデータの特徴はわからないので、度数分布表とヒストグラムを作って見ていきます。
Rではヒストグラムと同時に度数分布表のデータを取得できる
早速、度数分布表を作ってヒストグラムを描いてみますが・・・
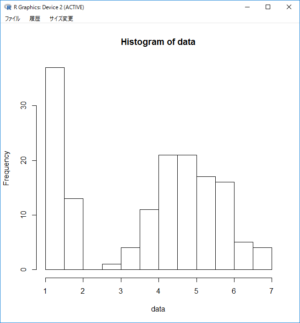
Rではヒストグラムを出力する関数(hist)を使うと、度数分布表を作らずにヒストグラムを描くことができます。
hist(data)
ここまではRの基本で教科書レベルですが、実はhist関数にはヒストグラムの元になった、度数分布表のデータが収納されています。
このデータを取り出して、度数分布表も作ってみます。
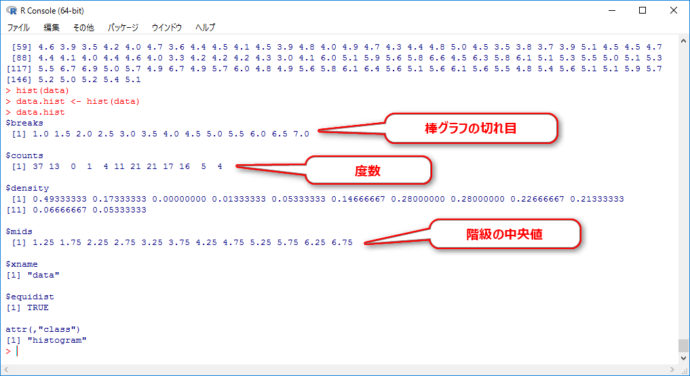
data.hist <- hist(data) data.hist
hist関数が持っているデータを新たに「data.hist」に保存することで、その中身を見ることができます。
このデータにはヒストグラムの元になっている度数分布に関するデータが入っているので、そのまま転用すれば度数分布表を簡単に作ることができます。
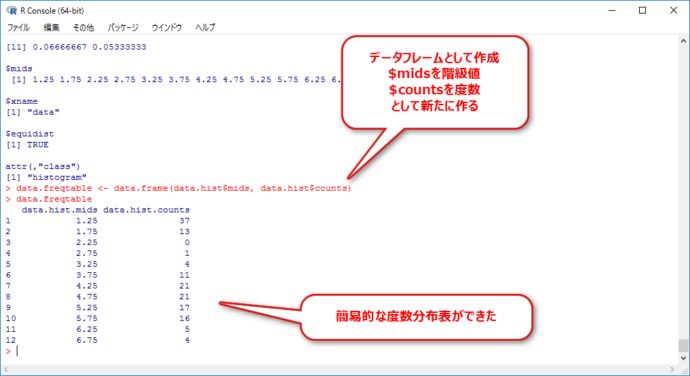
data.freqtable <- data.frame(data.hist$mids, data.hist$counts) data.freqtable
ここまでできれば後は相対度数・累積相対度数を計算するだけです。
相対度数はデータの数で度数を割る、累積相対度数は単に累積値を求めればいいので、データフレームにその列を組み込みます。
relaFreq <- data.hist$counts / length(data) * 100 # 相対度数 cumsumRelaFreq <- cumsum(relaFreq) # 累積相対度数 data.freqtable <- data.frame(data.freqtable, relaFreq, cumsumRelaFreq) # 度数分布表につなげる data.freqtable # 表示
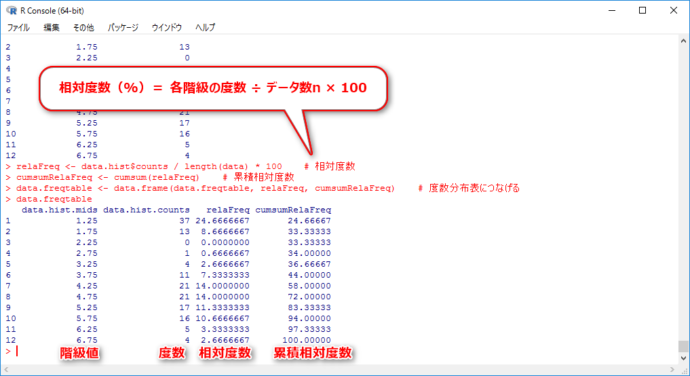
length関数はデータの個数(n)を求める関数、cumsum関数は累積和を求める関数です。
出来上がったベクトルを最後にデータフレームとして度数分布表にくっつけています。
これでヒストグラムと度数分布表が作れたので、一連の作業は終了です。
ヒストグラム・度数分布表から読み取れること
データ解析に戻って、最初のテーマにしていた、ヒストグラムから特徴つかむところに入っていきます。
無償配布のデータから流用していますが、こういう前提で見てみましょう。
太郎くんは花壇に咲いていた150本のあやめの花びらの長さを測って記録しました。
このデータについて、ヒストグラムと度数分布表から考えられることは何でしょうか?
そう思いながら、ヒストグラムと度数分布表を見てみます。
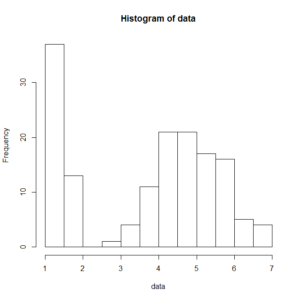
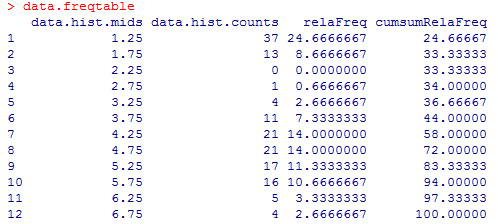
1cmの辺りと4,5cmの辺りに、山型が2つあります。
こういう形状を示しているときは、2種類のデータが混ざっていることを疑ってみます。
「1cmくらいの花びらのあやめ」と「4,5cmくらいの花びらのあやめ」は種類が違うあやめなのではないか?
と考えられるわけです。
ということは、1cmと4,5cmくらいのもので、グループ分けをしておいた方が良さそうだ!と考えることができます。
次に考えるのが、正規分布を仮定して統計処理を進めてよいか?です。
1cmと4,5cmの2つのグループに分けて考えるとき、それぞれのヒストグラムは山型なので、これも問題無いと思われます。
このあと、何かしらの統計的な処理をする場合は、正規分布を仮定した統計処理をしても良さそうです。
厳密には「正規性の検定」というのがあるのですが、この辺りは今は無視しておきます。
正規分布を仮定できるのであれば、平均値と標準偏差を利用すれば、代表値としては問題なさそうです。
逆に最頻値や中央値は使わないほうがいいかもしれません。
あとがき
今回はRの使い方も含めて、ヒストグラムの作り方と考え方を説明してみました。
もしRで統計を学ぶことを考えているならこの本が参考になるので、勉強したい方にはおすすめです。