代表値の意味は、データの特徴を表す数値の中でデータの中心となる値のことです。
イメージとしてはヒストグラムを描いたときの山になっている部分と捉えるとわかりやすいですね。
一般的には平均値と呼ばれる中心を使うこともい多いですが、その他に最頻値や中央値というのもあります。
それぞれ、利用する場面が違っているのでそのあたりはよく理解しておいたほうがいいと思います。
代表値の求め方と対応するRの関数
はじめに代表値について、サラッとまとめておきますね。
代表値 | 説明 | Rの関数 |
|---|---|---|
| 平均値(算術平均) | 全部のデータを足してデータの数で割れば求められる。 $latex \bar{x}=\frac{1}{n}\sum^{n}_{i=1}x_i&s=2$ | mean() |
| 中央値 | データを小さい順に並べ、両側からちょうど真ん中にある数値のこと。 奇数個の数値からできているデータであれば真ん中。 偶数個の数値からできているデータでは真ん中2つの値の平均値。 | median() |
| 最頻値 | データの中で最も多く現れる数値または文字などの記号。 | table() → 標準機能 mfv() → modeestパッケージ |
代表値の求め方と実際のRの使い方
ここから先で使えるように予めデータを用意しておきましょう。
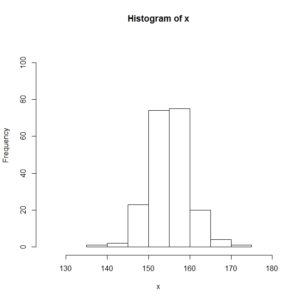
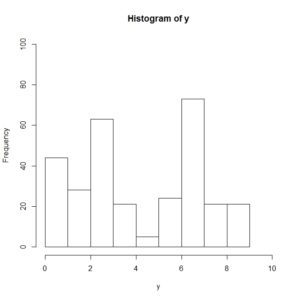
連続型データとしてx、離散型データとしてyを用意します。
x <- rnorm(200, mean=155, sd=5) yprob <- c(0.05, 0.07, 0.09, 0.21, 0.07, 0.03, 0.08, 0.25, 0.1, 0.05) y <- sample(0:9, 300, replace=TRUE, prob=yprob)
yprobはyを用意するためのベクタなので気にしないでOKです。
ヒストグラムを書いてみるとこんなデータです。
このデータに対して代表値を求めていきます。
平均値の求め方
平均値は基本統計量の中でもよく使われるもので、データの数値をすべて足してデータの個数で割ったものです。
数学的には
$latex \bar{x}=\frac{x_1+x_2+x_3+\cdots+x_n}{n}=\frac{1}{n}\sum^{n}_{i=1}x_i&s=3$
と表現されます。
ちなみに、数学では平均値のことを「$latex \bar{x}&s=1$」のように表現して、「エックス・バー」と読みます。
平均値は数学的な四則演算ができなければ求めることはできないので、普通は連続型のデータに用います。
ほとんどのデータで代表値といえば、この平均値が使われていますね。
Rを使った平均値の求め方【mean関数】
Rで平均値を求めるには、mean関数という関数を使ってこう入力します。
mean(x)
Rの電卓的な書き方で平均値を求めるには次のようにします。
sum(x)/length(x)
length関数はデータの個数を求める関数、sum関数は合計を求める関数です。
mean関数で求めた結果と同じになっているはずです。
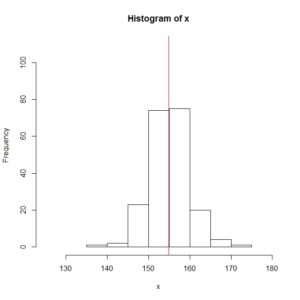
求めた平均値をヒストグラムに書き加えるには abline関数を使います。
abline(v=mean(x), col="red")
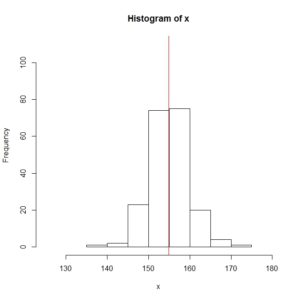
abline関数は元々「$latex y=ax+b&s=1$」の直線を引くための関数ですが、 「v=数値」とするとx軸に垂直(バーティカル;vertical)な直線、グラフ上では「$latex x=v&s=1$」の直線を引くことができます。
中央値の求め方
中央値は観測データを大小で並べ替えて、ちょうど真ん中に来た値のことを言います。
観測データとして、「$latex y=(y_1, y_2, y_3, \cdots, y_n)&s=1$」というn個のデータが得られたとします。
これを小さい順に並べ替えたものを「$latex y’=(y’_1, y’_2, y’_3, \cdots, y’_n)&s=1$」として置き換えると、中央値「$latex Q_{\frac{1}{2}}&s=1$」はこうなります。
$latex Q_{\frac{1}{2}}=y’_{\frac{n+1}{2}}&s=3$ $latex n&s=2$ が奇数の場合
$latex Q_{\frac{1}{2}}=\frac{1}{2}(y’_{\frac{n}{2}}+y’_{\frac{n}{2}+1})&s=3$ $latex n&s=2$ が偶数の場合
ただ、この方法をRのようなソフト無しでやろうとするとなかなか骨が折れるので、手計算はふつうしませんね。
Rを使った中央値の求め方【median関数】
Rで中央値を求めるにはmedian関数を使って
median(x)
とすると求められます。
Rの計算機能で求めようとするには、これば正確ではありませんが、次のようにします。
xs <- sort(x) xs[floor(length(xs)/2)]
中央値はデータの長さ(個数)が奇数個のとき、ちょうど真ん中の値を得ることができますが、データの長さが偶数個の場合は、真ん中の2つの値の平均値となるように求めるのが一般的です。
なので、このように計算機能を使って求めるよりmedian関数を使うことをおすすめします。
求めた中央値をヒストグラムに追加するにはabline関数を使って、平均値と同じようにします。
abline(v=median(x), col="red")
最頻値の求め方
最頻値はデータの中で一番多く出現した値のことを言います。
数式的には確率密度関数など複雑な話が出てくるので、ここでは割愛します。
例としてはある観測値「$latex x&s=1$」が
$latex x=(1, 2, 3, 3, 3, 4, 4, 5)&s=3$
となったとき、一番多く出現した「3」を最頻値(モード; mode)と呼びます。
Rを使った最頻値の求め方【table関数】
Rでは最頻値を直接求める用途の関数はありませんが、table関数という観測値を集計する関数があります。
これを利用して最頻値を求めることができます。
yt <- table(y)
yt[yt == max(yt)]
Rの初心者の方には難しいかもしれませんが、Rをインストールした時点ですぐ使える方法がこの方法です。
何をしているのかというと、table関数で集計したデータの中で、一番多く観測された値とその頻度を集計表から取り出すことをしています。
その部分が”[yt == max(yt)]”の部分です。
ちょっとテクニカルなのですが、はじめのうちはこのくらいの処理ができるようになれば十分です。
単純にtable関数の結果だけでも充分な場合もあるので、そのあたりは臨機応変にしてください。
Rを使った最頻値の求め方【modeestパッケージ:mfv関数】
最頻値を直接求めるにはmodeestパッケージのmfv関数を使うこともできます。
頻繁に最頻値を出力したい場合はこちらのほうが楽かもしれません。
これを使うには、modeestパッケージをインストールして、library関数で読み込む必要があります。
読み込みはこうします。
library(modeest)
library関数で読み込んでからmfv関数を使用します。
mfv(y)
とすれば最頻値を求めることができます。
結局手間がかかる作業なので、アンケート調査などで最頻値が常に必要になる場合に使うことをおすすめします。